Why Attention needs the three musketeers - Query, Key and Value
In the landmark paper “Attention is all you need” we were introduced to the Transformer architecture which forever “transformed” how large language models are trained using deep neural networks. The “near-human” level performance of LLMs is possible due to terabytes and petabytes of data used in training which in turn is made possible due to the shift from RNN/LSTM to the Attention achitecture.
Attention Is All You Need
RNN and its variants such as LSTM and GRU are sequential in nature i.e. for a given sequence of length L > 1, the hidden representation for the token (or word) at index i > 0 is dependent on the representations and some contexts learned from the tokens at indices 0 to i-1. Since each token at index i already “encodes” information from 0 to i-1, thus for calculating the representation for token at index i+1, we can only use the representation for index i instead of all previous indices (something similar to Markov Chain).
Thus we see that it is not possible to calculate the representation for token say 10 without calculating the representation for token 5.
On the other hand, Attention mechanism allows one to calculate the representation for token 10 before calculating the representation for token 5 and thus allowing the representations to be computed in parallel. This is in turn is made possible due to the 3 different vectors for each token namely, Query, Key and Value.
The idea is to calculate the representation R(i) for the token at index i as a function of some vectors V(j) corresponding to each token j where the vectors V(j) does not get updated in the same forward pass. If V(j) got updated in the same forward pass, then it would be again sequential. The simplest mechanism to calculate R(i) is to use a weighted sum of the V(j)’s i.e.
R(i,t) = w(0,t-1) * V(0,t-1) + w(1,t-1) * V(1,t-1) + ... + w(n-1,t-1) * V(n-1,t-1)
Note that this may not be the only way but probably the most simple way. For e.g. one can also concatenate the vectors V(j) but if the sequence length is very long, the resultant vector would also be very long.
The index ‘t’ denotes the epoch number. The above equation denotes that the representation for current epoch t and token index i is dependent only on weights w and vectors V from the previous epoch t-1.
The weights w(j) respresents the importance of the j-th token for predicting the i-th token in the sequence and it should be some function of the current token index i, else if w(j) was independent of i in the above equation, then for all indices i, R(i) would be same. One possible mechanism is to have another vector Q(j) corresponding to each token index j and then w(j) = <Q(i), Q(j)> i.e. dot product of Q(i) and Q(j).
Thus
R(i,t) = <Q(i, t-1), Q(0, t-1)> * V(0,t-1)
+ <Q(i, t-1), Q(1, t-1)> * V(1,t-1) +
+ .........
+ <Q(i, t-1), Q(n-1, t-1)> * V(n-1,t-1)
But note that the dot product <Q(i), Q(j)> is symmetric w.r.t i and j i.e.
<Q(i), Q(j)> = <Q(j), Q(i)>
The weights may not be symmetric in a sequence of tokens. For e.g. for the sequence “My phone has a RAM of 6GB”, the score of the token “phone” w.r.t. the token “RAM” need not be same as the score of the token “RAM” w.r.t. “phone” because “RAM” could also score highly with some other tokens such as “computer” or “laptop” etc. elsewhere in the input sequence. Thus, there is no need for the dot product to be symmetric.
The simplest way to extend this logic is to introduce another vector K(j) corresponding to each token index j and then the dot product is calculated as: <Q(i), K(j))>.
Thus
R(i,t) = <Q(i, t-1), K(0, t-1)> * V(0,t-1)
+ <Q(i, t-1), K(1, t-1)> * V(1,t-1)
+ ...
+ <Q(i, t-1), K(n-1, t-1)> * V(n-1,t-1)
One can easily verify that the dot products <Q(i), K(j))> are not symmetric i.e.
<Q(i), K(j)> != <Q(j), K(i)>
Note that the calculations for R(i,t) can be easily parallelized as each i are independent. R(i,t) only depends on parameters from the epoch t-1. Moreover one can conveniently represent the vectors in the form of matrices and the products and summations as matrix multiplications or dot product operations. This enables us to use fast matrix libraries such as BLAS with CPU and cuBLAS with GPUs. Numpy and Scipy uses BLAS in the backend to optimize matrix operations.
BLAS
Assuming that there are N tokens and the matrices Q, K and V are all of dimensions d, then Q, K, V and R are all of shape (N, d)
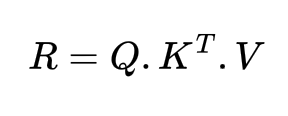
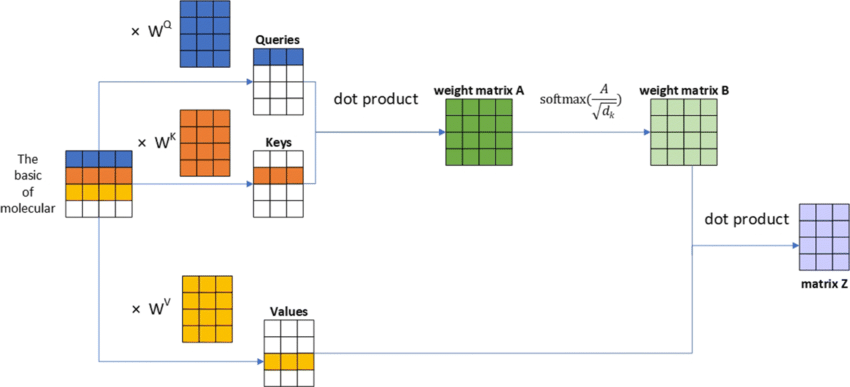
Note that the actual implementation of Attention differs from this derivation because there are few things we have not taken care of such as converting the weights into probability scores using a softmax function and normalizing the weights by the square root of the vector dimensions. The actual formula for the attention scores looks something like:
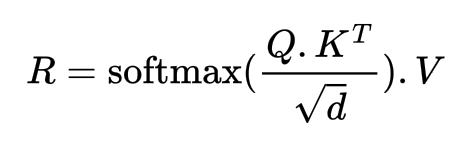
Sample implementation of the attention representations in C++ and OpenMP (for CPU parallelization):
void dot_product(
float *a,
float *b,
float *c,
const unsigned int nr_a,
const unsigned int nc_a,
const unsigned int nr_b,
const unsigned int nc_b) {
assert(nc_a == nr_b);
for (unsigned int i = 0; i < nr_a*nc_b; i++) c[i] = 0.0;
omp_set_num_threads(8);
#pragma omp parallel for shared(a, b, c)
for (unsigned int i = 0; i < nr_a; i++) {
for (unsigned int j = 0; j < nc_a; j++) {
for (unsigned int k = 0; k < nc_b; k++) {
c[i*nc_b+k] += a[i*nc_a+j]*b[j*nc_b+k];
}
}
}
}
void dot_product_b_transpose(
float *a,
float *b,
float *c,
const unsigned int nr_a,
const unsigned int nc_a,
const unsigned int nr_b,
const unsigned int nc_b) {
assert(nc_a == nc_b);
for (unsigned int i = 0; i < nr_a*nr_b; i++) c[i] = 0.0;
omp_set_num_threads(8);
#pragma omp parallel for shared(a, b, c)
for (unsigned int i = 0; i < nr_a; i++) {
for (unsigned int k = 0; k < nr_b; k++) {
float h = 0.0;
for (unsigned int j = 0; j < nr_b; j++) {
h += a[i*nc_a+j]*b[k*nc_b+j];
}
c[i*nr_b+k] = h;
}
}
}
void softmax(
float *scores,
const unsigned int n,
const unsigned int m) {
float *row_sum = new float[n];
float *row_max = new float[n];
for (unsigned int i = 0; i < n; i++) {
row_sum[i] = 0.0;
row_max[i] = -MAXFLOAT;
}
for (unsigned int i = 0; i < n*m; i++) row_max[i/m] = max(row_max[i/m], scores[i]);
for (unsigned int i = 0; i < n*m; i++) row_sum[i/m] += exp(scores[i]-row_max[i/m]);
for (unsigned int i = 0; i < n*m; i++) scores[i] = exp(scores[i]-row_max[i/m])/row_sum[i/m];
}
void score_transform(
float *scores,
const unsigned int n,
const unsigned int m,
const unsigned int d) {
assert(d > 0);
for (unsigned int i = 0; i < n*m; i++) scores[i] /= sqrt(d);
softmax(scores, n, m);
}
void attention(
float *Q,
float *K,
float *V,
float *R,
const unsigned int n,
const unsigned int d) {
float *scores = new float[n*n];
dot_product_b_transpose(Q, K, scores, n, d, n, d);
score_transform(scores, n, n, d);
dot_product(scores, V, R, n, n, n, d);
}