Parallelizing sequential algorithms on GPU - Prefix Sum
GPUs are highly effective in parallelizing algorithms more importantly algorithms which are inherently parallelizable as the ones we saw previously such as vector addition, matrix multiplication, convolution, histogram reduction etc. We also saw a GPU implementation of summation of an array of numbers. Unlike matrix multiplication or convolution where each thread is responsible for calculating independent or disjoint set of output values, summation of an array of numbers required only 1 output value and thus required synchronization between multiple threads. But with reduction tree technique and atomic addition it was relatively straightforward to achieve better performance on a GPU as compared to a CPU.
GPU Notes Part 1
GPU Notes Part 2
Given an input array A of N numbers, prefix sum return an array P of size N where P[i] is the summation from A[0] to A[i]. This is pretty straightforward to calculate using C/C++ as shown below:
void prefix_sum(float *A, float *P, unsigned int n) {
for (unsigned int i = 0; i < n; i++) {
if (i == 0) P[i] = A[i];
else P[i] = P[i-1] + A[i];
}
}
The time complexity of the above algorithm is O(N).
If we use separate threads to calculate the prefix sums for each index i in the output array P, then for the last index i.e. P[N-1], the corresponding thread needs to calculate the sum of all numbers in the input array A. Thus the worst case time complexity is still O(N) assuming each thread is running in parallel.
__global__
void prefix_sum_cuda_unoptimized(float *A, float *P, unsigned int n) {
unsigned int index = blockIdx.x*blockDim.x + threadIdx.x;
float sum = 0.0f;
for (unsigned int i = 0; i <= index; i++) {
sum += A[i];
}
if (index < n) P[index] = sum;
}
On the other hand total work done across all threads is O(N^2). But with large N, not all threads will be running in parallel as blocks are scheduled in streaming multiprocessors according to available resources. Thus, worst case time complexity is greater than O(N).
Thus each thread working independently will have a performance that is worse than the sequential algorithm implementation. On the other hand if for each index i, all threads collaborate to calculate the sum from A[0] to A[i] just like the summation problem using a reduction tree, then although calculation for each index is optimized but overall we still need to calculate with all indices in a sequential manner leading to a performance that is again worse than the sequential algorithm.
An alternative stratgey would be to use a combination of the 2 approaches above i.e. each thread independently calculates the prefix sums for a block of the array A and then later collaborate to merge the block prefix sums. Two popular algorithms exists for the same. One is known as the Kogge-Stone algorithm and the other is the Brent-Kung algorithm. Both the algorithms are used in digital circuit design for implementing adders.
Kogge Stone Adder
Brent Kung Adder
Let’s start with the Kogge Stone adder first. The diagrammatic representation is shown below. The algorithm works in stages as follows:
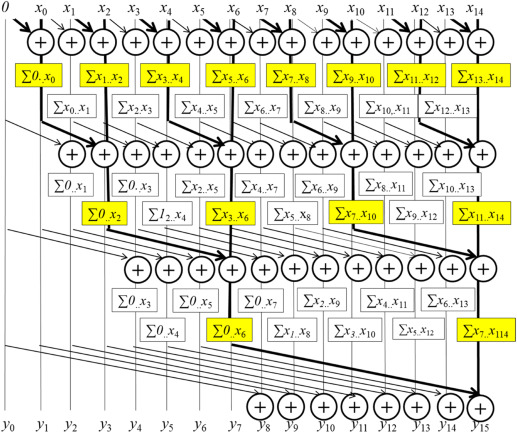
Copy the input array A in the output array P. Then for each stage S (starting from 0), for each index i greater than equal to (1<<S) i.e. 2 to the power of S, in the output array P, calculate the sum P[i] = P[i]+P[i-(1<<S)]
At the end of log2(N) stages, each index i will contain the sum of A[0] to A[i].
Let’s implement the above in CUDA as follows:
__global__
void prefix_sum_kogge_stone(float *A, float *P, int n) {
unsigned int index = blockIdx.x*blockDim.x + threadIdx.x;
if (index < n) P[index] = A[index];
for (unsigned int stride = 1; stride < blockDim.x; stride *= 2) {
float temp = 0.0f;
if (threadIdx.x >= stride) temp = P[threadIdx.x-stride];
__syncthreads();
P[threadIdx.x] += temp;
__syncthreads();
}
}
In the above code we are using a temp variable to store the results of P[threadIdx.x-stride] before updating P[threadIdx.x] because for e.g. if stride=2 and threadIdx.x=5, then the thread will add P[3] to P[5] and update P[5]. But since threads are running in parallel, it could be possible that the thread with threadIdx.x=3, is also updating P[3] = P[3] + P[1]. Now if threadIdx.x=3 updates P[3] before threadIdx.x=5 reads P[3] we will have incorrect value stored in P[5] as P[5] requires the older value of P[3] and not the current value. Hence we first need to read all the older values in thread specific registers (float temp) and then after all threads have stored these values, we update the values.
But note that the above code will only work correctly if there is only 1 block of thread. But since a block can have a maximum upto 1024 threads thus the above code is only able to handle array sizes N <= 1024. But why this is so ?
Assuming we are having multiple blocks and each block contains 1024 threads, now for the index say 1025 i.e. block index=1 and stride=4, the update equation will look like P[1025] = P[1025] + P[1021].
But note that index=1021 lies in block=0 while index=1025 in block=1 and __syncthreads() is only applicable at the block level i.e. the threads corresponding to indices 1021 and 1025 will not be synchronized and as a result P[1025] might read the updated value of P[1021] instead of the old value leading to incorrect results.
Block synchronization is a tricky affair in CUDA as not all blocks will be running in parallel. If number of blocks are greater than the number of streaming multiprocessors, then only a subset of all blocks will be running in parallel. The rest of the blocks will wait for their turn.
__device__ unsigned int counter = 0
__global__
void prefix_sum_kogge_stone(float *A, float *P, int n) {
unsigned int index = blockIdx.x*blockDim.x + threadIdx.x;
if (index < n) P[index] = A[index];
for (unsigned int stride = 1; stride < blockDim.x; stride *= 2) {
float temp = 0.0f;
if (threadIdx.x >= stride) temp = P[threadIdx.x-stride];
// synchronize all threads across all blocks
while (atomicAdd(&counter, 1) < blockDim.x*gridDim.x) {}
P[threadIdx.x] += temp;
// synchronize all threads across all blocks
while (atomicSub(&counter, 1) > 0) {}
}
}
A common way to synchronize all threads across all blocks is to use a while () {} loop like the one shown above. Using a global variable counter, each threads takes turn to update its value and when all thread updates the value only then the current thread is able to break out of the while loop. A common danger in the above code is when number of SMs are smaller than the number of blocks in which case we might see a deadlock happening.
Synchronizing all threads across all blocks penalize performance heavily. An alternative way to implement the Kogge-Stone algorithm is to run the algorithm per block first. After this all blocks would have computed its own prefix sums. Except for the 1st block all other blocks will have only partial prefix sums.
Using a global array S of length equal to the number of blocks, each index i in S stores the value of the prefix sum from the last index for each block. Thus each element of S corresponds to the sum of one block.
Then run the prefix sum algorithm again but now on the global array S.
Then for each block, for each index i add the value of S[blockIdx.x-1] i.e. the value of S corresponding to the previous block to itself. In this way each output element will have the correct value.
Taking an example:
Input : A = [2,1,5,8,9,0,4,6,3,4,5,4,1,7,7,2]
block size = 4
STEP 1: Calculate P array for each block
A0 = [2,1,5,8] P0 = [2,3,8,16]
A1 = [9,0,4,6] P1 = [9,9,13,19]
A2 = [3,4,5,4] P2 = [3,7,12,16]
A3 = [1,7,7,2] P3 = [1,7,15,17]
STEP 2: Calculate S array from last elements of each P above
S = [16, 19, 16, 17]
STEP 3: Calculate prefix sum array for S from Step 2
PS = [16, 35, 51, 68]
STEP 3: Update P array for each block using the prefix sum S array PS above
P0' = P0 = [2, 3, 8, 16]
P1' = P1 + PS[0] = [9+16, 9+16, 13+16, 19+16] = [25, 25, 29, 35]
P2' = P2 + PS[1] = [3+35, 7+35, 12+35, 16+35] = [38, 42, 47, 51]
P3' = P3 + PS[2] = [1+51, 7+51, 15+51, 17+51] = [52, 58, 66, 68]
STEP 5: Concatenate the P arrays
P = [2, 3, 8, 16, 25, 25, 29, 35, 38, 42, 47, 51, 52, 58, 66, 68]
Instead of running prefix sum algorithm twice, once on A and once on S in the above algorithm, one can modify the above algorithm as follows:
After step 1, for each block check if the S element corresponding to the previous block i.e. S[blockIdx.x-1] has been computed. If the S element in the previous block has been computed, then update the S element of current block by adding S[blockIdx.x-1] to the last element of its P array. After that, update all indices for P in the current block by adding S[blockIdx.x-1].
Input : A = [2,1,5,8,9,0,4,6,3,4,5,4,1,7,7,2]
block size = 4
STEP 1: Calculate P array for each block
A0 = [2,1,5,8] P0 = [2,3,8,16]
A1 = [9,0,4,6] P1 = [9,9,13,19]
A2 = [3,4,5,4] P2 = [3,7,12,16]
A3 = [1,7,7,2] P3 = [1,7,15,17]
STEP 2: Calculate S array from last elements of P above and previous blocks' S value.
S0 = 0 + 16 = 16 P0 = [2, 3, 8, 16]
S1 = 16 + 19 = 35 P1 = [9+16, 9+16, 13+16, 19+16] = [25, 25, 29, 35]
S2 = 35 + 16 = 51 P2 = [3+35, 7+35, 12+35, 16+35] = [38, 42, 47, 51]
S3 = 51 + 17 = 68 P3 = [1+51, 7+51, 15+51, 17+51] = [52, 58, 66, 68]
STEP 3: Concatenate the P arrays
P = [2, 3, 8, 16, 25, 25, 29, 35, 38, 42, 47, 51, 52, 58, 66, 68]
The calculations using Kogge-Stone can be further optimized by using shared memory array. In order to identify whether the S element corresponding to previous block has been computed or not, we use another flags array where flags[blockIdx.x]=1 if S corresponding to blockIdx.x has been computed, else flags[blockIdx.x]=0.
In the below code we use the logic discussed above but with a small change that each block updates the S element for the next block by adding the S value of the current block to it. Similarly for the flags boolean array. This doesn’t change the algorithm only the block indices are shifted. The code is as follows:
#define BLOCK_WIDTH 1024
__device__
void prefix_sum_kogge_stone_block(
float *A,
float *XY,
unsigned int n) {
unsigned int index = blockIdx.x*blockDim.x + threadIdx.x;
if (index < n) XY[threadIdx.x] = A[index];
else XY[threadIdx.x] = 0.0f;
__syncthreads();
for (unsigned int stride = 1; stride < blockDim.x; stride *= 2) {
float temp = 0.0f;
if (threadIdx.x >= stride) temp = XY[threadIdx.x-stride];
__syncthreads();
XY[threadIdx.x] += temp;
__syncthreads();
}
}
__global__
void prefix_sum(
float *A,
float *P,
int *flags,
float *S,
unsigned int n,
unsigned int m) {
extern __shared__ float XY[];
unsigned int index = blockIdx.x*blockDim.x + threadIdx.x;
// calculate kogge-stone algorithm per blcok and store the
// results in a shared memory array
prefix_sum_kogge_stone_block(A, XY, n);
// since S is updated once per block, thus the below code runs
// only for the 1st thread in each block
if (blockIdx.x + 1 < m && threadIdx.x == 0) {
// check if the previous block has set the S element
// corresponding to current block.
// if not then continue while loop else break loop.
while (atomicAdd(&flags[blockIdx.x], 0) == 0) {}
// update the S element for the next block by adding the S element of
// current block with the last element of XY shared memory array
S[blockIdx.x + 1] = S[blockIdx.x] + XY[min(blockDim.x-1, n-1-blockIdx.x*blockDim.x)];
// __threadfence() indicates that any other block will
// see the change in S before the change in flag set below.
__threadfence();
// set the flag for the next block
atomicAdd(&flags[blockIdx.x + 1], 1);
}
// syncing threads is required here because we are reading one index of XY
// above and updating a different index of XY below.
__syncthreads();
if (blockIdx.x < m && blockIdx.x > 0) {
// check if the flag is set for current block which
// implies that the S element is also updated.
while (atomicAdd(&flags[blockIdx.x], 0) == 0) {}
// update XY shared memory array for all threads in the current block
XY[threadIdx.x] += S[blockIdx.x];
}
// finally update the global memory array P with XY shared memory array.
// __syncthreads() is not required here because we are updating XY[threadIdx.x]
// above and also reading from XY[threadIdx.x] below.
if (index < n) P[index] = XY[threadIdx.x];
}
int main(){
int n = 1e7;
int m = int(ceil(float(n)/BLOCK_WIDTH));
float *A, *S, *P;
int *flags;
cudaMallocManaged(&A, n*sizeof(float));
cudaMallocManaged(&P, n*sizeof(float));
cudaMallocManaged(&S, m*sizeof(float));
cudaMallocManaged(&flags, m*sizeof(int));
for (int i = 0; i < m; i++) S[i] = 0.0;
for (int i = 0; i < m; i++) flags[i] = 0;
flags[0] = 1;
prefix_sum<<<m, BLOCK_WIDTH, BLOCK_WIDTH*sizeof(float)>>>(A, P, flags, S, n, m);
cudaDeviceSynchronize();
}
Considering each block, total number of strides in the Kogge-Stone algorithm is log2(BLOCK_WIDTH). Total work done across all threads can be calculated as follows:
STRIDE = 1, Num Active Threads = BLOCK_WIDTH-1
STRIDE = 2, Num Active Threads = BLOCK_WIDTH-2
STRIDE = 4, Num Active Threads = BLOCK_WIDTH-4
....
STRIDE = 2^(K-1), Num Active Threads = BLOCK_WIDTH-2^(K-1)
K = log2(BLOCK_WIDTH)
Total work done by threads = (BLOCK_WIDTH-1) + (BLOCK_WIDTH-2) + ... + (BLOCK_WIDTH-2^(K-1))
= K*BLOCK_WIDTH - (1+2+...+2^(K-1))
= BLOCK_WIDTH*(K-1)
Assuming that only Q threads per block can run in parallel (due to resource constraints), then the run-time complexity for the Kogge-Stone algorithm per block is BLOCK_WIDTH*(K-1)/Q. In the case where we have sufficient resources then Q=BLOCK_WIDTH, then run-time complexity is K-1 where K is defined as above. The analysis can easily scaled to all the elements in the array A by scaling BLOCK_WIDTH with number of blocks.
Thus, in the worst case where Q is a small constant as compared to N, the run time complexity is O(NlogN).
The other algorithm i.e. Brent-Kung algorithm is bit trickier to understand but often performs better than the Kogge-Stone algorithm described above. The algorithm works in 2-stages as follows:
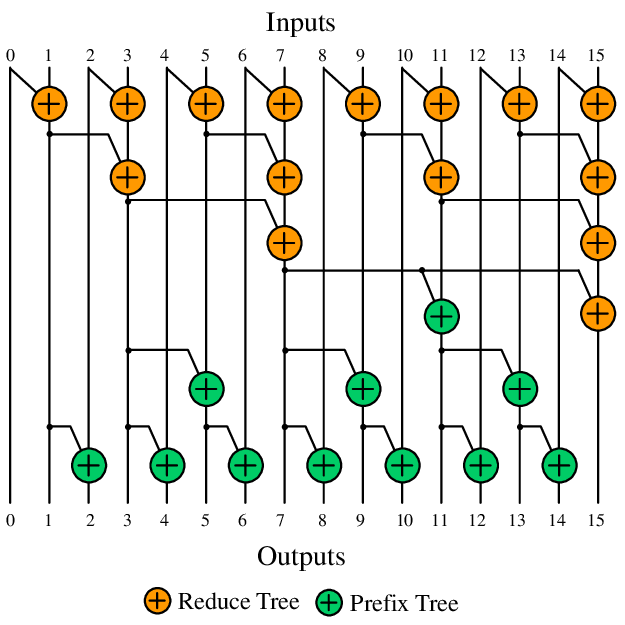
In the first stage, each thread runs with multiple strides similar to the Kogge Stone algorithm. Assuming the algorithm runs per block, the thread with index i and stride=S will add up indices j=2*(i+1)*S-1 and j-S and store the result in the index j, i.e.
P[j] += P[j-S] where j=2*(i+1)*S-1
The strides increases from 1 to BLOCK_WIDTH by repeatedly multiplying with 2.
In the next stage, the thread with index i and stride=S, will add up the indices j=2*(i+1)*S-1 and j+S and store the result in the index j+S, i.e.
P[j+S] += P[j] where j=2*(i+1)*S-1
But in the 2nd stage, the strides S starts from BLOCK_WIDTH/4 and decreases to 1 in subsequent iterations by repeatedly dividing by 2.
The CUDA device code for Brent-Kung algorithm is as follows. To run the prefix_sum algorithm using Brent-Kung algorithm just replace prefix_sum_kogge_stone_block with prefix_sum_brent_kung_block in the above prefix_sum kernel above:
#define BLOCK_WIDTH 1024
__device__
void prefix_sum_brent_kung_block(
float *A,
float *XY,
unsigned int n) {
// Load the input array in shared memory
unsigned int index = blockIdx.x*blockDim.x + threadIdx.x;
if (index < n) XY[threadIdx.x] = arr[index];
else XY[threadIdx.x] = 0.0f;
__syncthreads();
// Reduction tree in 1st stage computed using strides
for (unsigned int stride = 1; stride < blockDim.x; stride *= 2) {
int i = 2*(threadIdx.x+1)*stride-1;
if (i < BLOCK_WIDTH && i >= stride) XY[i] += XY[i-stride];
__syncthreads();
}
// Reduction tree in 2nd stage computed using strides
for (unsigned int stride = BLOCK_WIDTH/4; stride > 0; stride /= 2) {
int i = 2*(threadIdx.x+1)*stride-1;
if (i + stride < BLOCK_WIDTH) XY[i + stride] += XY[i];
__syncthreads();
}
}
Considering each block, total number of strides in the Brent-Kung algorithm in 1st stage is log2(BLOCK_WIDTH). Total work done across all threads can be calculated as follows:
STRIDE = 1, Num Active Threads = BLOCK_WIDTH/2
STRIDE = 2, Num Active Threads = BLOCK_WIDTH/4
STRIDE = 4, Num Active Threads = BLOCK_WIDTH/8
....
STRIDE = 2^(K-1), Num Active Threads = BLOCK_WIDTH/(2^K)
K = log2(BLOCK_WIDTH)
Total work done by threads = BLOCK_WIDTH/2 + BLOCK_WIDTH/4 + ... + BLOCK_WIDTH/(2^K)
= BLOCK_WIDTH/2*(1+1/2+1/4+...+1/(2^(K-1)))
= BLOCK_WIDTH*(1-1/2^K)
Assuming that only Q threads per block can run in parallel (due to resource constraints), then the run-time complexity for the Brent-Kung algorithm per block is BLOCK_WIDTH*(1-1/2^K)/Q. In the case where we have sufficient resources then Q=BLOCK_WIDTH, then run-time complexity is 1-1/2^K where K is defined as above.
Thus, in the worst case where Q is a small constant as compared to N, the run time complexity is O(N). In the best case it is almost O(1). But rarely we will see this because there are other overheads in the process such as syncing threads per block, syncing threads across blocks etc. which is where most time goes into. As number of elements increases, number of threads required also increases and thus syncing the threads increases in complexity.
The above algorithms can be improved further by using thread coarsening as shown below. Each thread is responsible for calculating the prefix sums for COARSE_FACTOR number of elements. The full code using thread coarsening for Brent-Kung algorithm is shown below:
#define BLOCK_WIDTH 1024
#define COARSE_FACTOR 8
__device__
void prefix_sum_brent_kung_block_coarsened(
float *A,
float *XY,
unsigned int n) {
// Each thread is responsible for loading COARSE_FACTOR number of input elements
// into shared memory
for (unsigned int i = threadIdx.x; i < COARSE_FACTOR*blockDim.x; i += blockDim.x) {
unsigned int index = COARSE_FACTOR*blockIdx.x*blockDim.x + i;
if (index < n) XY[i] = A[index];
else XY[i] = 0.0f;
}
__syncthreads();
// Reduction tree in 1st stage computed using strides
// Each thread is responsible for COARSE_FACTOR number of elements
for (unsigned int stride = 1; stride < COARSE_FACTOR*blockDim.x; stride *= 2) {
for (unsigned int i = threadIdx.x; i < COARSE_FACTOR*blockDim.x; i += blockDim.x) {
int j = 2*(i+1)*stride-1;
if (j < COARSE_FACTOR*BLOCK_WIDTH && j >= stride) XY[j] += XY[j-stride];
}
__syncthreads();
}
// Reduction tree in 2nd stage computed using strides
for (unsigned int stride = COARSE_FACTOR*BLOCK_WIDTH/4; stride > 0; stride /= 2) {
for (unsigned int i = threadIdx.x; i < COARSE_FACTOR*blockDim.x; i += blockDim.x) {
int j = 2*(i+1)*stride-1;
if (j + stride < COARSE_FACTOR*BLOCK_WIDTH) XY[j + stride] += XY[j];
}
__syncthreads();
}
}
__global__
void prefix_sum_coarsened(
float *A,
float *P,
int *flags,
float *S,
unsigned int n,
unsigned int m) {
extern __shared__ float XY[];
prefix_sum_brent_kung_block_coarsened(A, XY, n);
if (blockIdx.x + 1 < m && threadIdx.x == 0) {
// wait for previous block to update S and pass it on.
while (atomicAdd(&flags[blockIdx.x], 0) == 0) {}
// update S and flags and pass to next block
S[blockIdx.x + 1] = S[blockIdx.x]
+ XY[min(COARSE_FACTOR*blockDim.x-1, n-1-COARSE_FACTOR*blockIdx.x*blockDim.x)];
__threadfence();
atomicAdd(&flags[blockIdx.x + 1], 1);
}
__syncthreads();
if (blockIdx.x < m && blockIdx.x > 0) {
while (atomicAdd(&flags[blockIdx.x], 0) == 0) {}
// update own shared memory array using S sent from previous block
for (unsigned int i = threadIdx.x; i < COARSE_FACTOR*blockDim.x; i += blockDim.x) {
XY[i] += S[blockIdx.x];
}
}
for (unsigned int i = threadIdx.x; i < COARSE_FACTOR*blockDim.x; i += blockDim.x) {
unsigned int index = COARSE_FACTOR*blockIdx.x*blockDim.x + i;
if (index < n) P[index] = XY[i];
}
}
int main(){
unsigned int n = 1e7;
unsigned int m = int(ceil(float(n)/(COARSE_FACTOR*BLOCK_WIDTH)));
float *A, *S, *P;
int *flags;
cudaMallocManaged(&A, n*sizeof(float));
cudaMallocManaged(&P, n*sizeof(float));
cudaMallocManaged(&S, m*sizeof(float));
cudaMallocManaged(&flags, m*sizeof(int));
for (unsigned int i = 0; i < m; i++) S[i] = 0.0;
for (unsigned int i = 0; i < m; i++) flags[i] = 0;
flags[0] = 1;
prefix_sum<<<m, BLOCK_WIDTH,
COARSE_FACTOR*BLOCK_WIDTH*sizeof(float)>>>(A, P, flags, S, n, m);
cudaDeviceSynchronize();
}
Although theorectically Brent-Kung algorithm could perform better than the sequential algorithm in the ideal world, but on my RTX 4050, with N=1e7 input elements the sequential algorithm takes around 20ms whereas the coarsened Brent Kung algorithm takes somewhere around 50ms i.e more than double the time.
This could be due to multiple reasons for e.g. the sequential nature of block message propagation to calculate the array S i.e. updating S per block and passing it to the next block, syncing the threads per block etc. Another per block performance bottleneck is the bank memory conflict in shared memory. Assuming that shared memory per blcok is divided into 32 banks each of 32-bits i.e. each floating point number maps to one of 32 banks in shared memory. A bank conflict occurs when two or more threads access different elements mapping to the same bank.
For a given warp of 32 threads if the threads accesses consecutive elements, we will not have bank conflicts but if they are accessed with strides of 1, 2, 4, 8 and so on as in Brent-Kung algorithm we will have bank conflicts as shown below:
Non-strided access in warp
Thread ID : 0 1 2 ... 15 16 17 18 ... 30 31
Arr Index : 0 1 2 ... 15 16 17 18 ... 30 31
Bank : 0 1 2 ... 15 16 17 18 ... 30 31
Elements read when stride = 1
Thread ID : 0 1 2 ... 15 16 17 18 ... 30 31
Arr Index : 0 2 4 ... 30 32 34 36 ... 60 62
Bank : 0 2 4 ... 30 0 2 4 ... 28 30
Arr indices 0 and 32 access bank 0
Arr indices 2 and 34 access bank 2
...
and so on.
Thus we have 2-way bank conflict when stride = 1
Elements read when stride = 2
Thread ID : 0 1 2 ... 7 8 9 ... 15 16 17 18 ... 30 31
Arr Index : 1 5 9 ... 29 33 37 ... 61 65 69 73 ... 121 125
Bank : 1 5 9 ... 29 1 5 ... 29 1 5 9 ... 25 29
Arr indices 1, 33, 65 and 97 all accesses bank 0
Arr indices 5, 37, 69 and 101 all accesses bank 5
...
and so on.
Thus we have 4-way bank conflict when stride = 2
One technique used in CUDA to avoid bank conflicts is using memory padding i.e. shift the indices in shared memory by some amount by filling in with dummy indices. For e.g. in the above strided access pattern, we pad the shared memory array indices 32, 64, 96 … with dummy values and shift the remaining indices right. Thus, what was at index 32 earlier will be at index 33 and so on. Similarly what was at index 64 earlier will now be at index 66 and so on.
Thus, an index i is mapped to the modified index i + i/32 in this schema or i + (i >> 5).
Elements read when stride = 1
Thread ID : 0 1 2 ... 15 16 17 18 ... 30 31
Arr Index : 0 2 4 ... 30 33 35 37 ... 61 63
Bank : 0 2 4 ... 30 1 3 5 ... 29 31
Elements read when stride = 2
Thread ID : 0 1 2 ... 7 8 9 ... 15 16 17 18 ... 30 31
Arr Index : 1 5 9 ... 29 34 38 ... 62 67 71 75 ... 124 128
Bank : 1 5 9 ... 29 2 6 ... 30 3 7 11 ... 28 0
The Brent-Kung code modified to use memory padding:
#define NUM_BANKS 32
#define LOG_NUM_BANKS 5
#define CONFLICT_FREE_OFFSET(n)((n) >> (LOG_NUM_BANKS))
#define BUFFER 255
__device__
void prefix_sum_brent_kung_block_coarsened(
float *A,
float *XY,
unsigned int n) {
for (unsigned int i = threadIdx.x; i < COARSE_FACTOR*blockDim.x; i += blockDim.x) {
unsigned int index = COARSE_FACTOR*blockIdx.x*blockDim.x + i;
unsigned int offset = CONFLICT_FREE_OFFSET(i);
if (index < n) XY[i + offset] = A[index];
else XY[i + offset] = 0.0f;
}
__syncthreads();
for (unsigned int stride = 1; stride < COARSE_FACTOR*blockDim.x; stride *= 2) {
for (unsigned int i = threadIdx.x; i < COARSE_FACTOR*blockDim.x; i += blockDim.x) {
int j = 2*(i+1)*stride-1;
unsigned int offset1 = CONFLICT_FREE_OFFSET(j);
unsigned int offset2 = CONFLICT_FREE_OFFSET(j-stride);
if (j + offset1 < COARSE_FACTOR*BLOCK_WIDTH + BUFFER && j + offset2 >= stride)
XY[j + offset1] += XY[j-stride + offset2];
}
__syncthreads();
}
for (unsigned int stride = COARSE_FACTOR*BLOCK_WIDTH/4; stride > 0; stride /= 2) {
for (unsigned int i = threadIdx.x; i < COARSE_FACTOR*blockDim.x; i += blockDim.x) {
int j = 2*(i+1)*stride-1;
unsigned int offset1 = CONFLICT_FREE_OFFSET(j+stride);
unsigned int offset2 = CONFLICT_FREE_OFFSET(j);
if (j + stride + offset1 < COARSE_FACTOR*BLOCK_WIDTH + BUFFER)
XY[j + stride + offset1] += XY[j + offset2];
}
__syncthreads();
}
}
__global__
void prefix_sum_coarsened(
float *A,
float *P,
int *flags,
float *S,
unsigned int n,
unsigned int m) {
extern __shared__ float XY[];
prefix_sum_brent_kung_block_coarsened(A, XY, n);
if (blockIdx.x + 1 < m && threadIdx.x == 0) {
while (atomicAdd(&flags[blockIdx.x], 0) == 0) {}
int j = min(COARSE_FACTOR*blockDim.x-1, n-1-COARSE_FACTOR*blockIdx.x*blockDim.x);
S[blockIdx.x + 1] = S[blockIdx.x] + XY[j + CONFLICT_FREE_OFFSET(j)];
__threadfence();
atomicAdd(&flags[blockIdx.x + 1], 1);
}
__syncthreads();
if (blockIdx.x < m && blockIdx.x > 0) {
while (atomicAdd(&flags[blockIdx.x], 0) == 0) {}
for (unsigned int i = threadIdx.x; i < COARSE_FACTOR*blockDim.x; i += blockDim.x) {
int j = i + CONFLICT_FREE_OFFSET(i);
XY[j] += S[blockIdx.x];
}
}
for (unsigned int i = threadIdx.x; i < COARSE_FACTOR*blockDim.x; i += blockDim.x) {
unsigned int index = COARSE_FACTOR*blockIdx.x*blockDim.x + i;
if (index < n) P[index] = XY[i + CONFLICT_FREE_OFFSET(i)];
}
}
int main(){
unsigned int n = 1e7;
unsigned int m = int(ceil(float(n)/(COARSE_FACTOR*BLOCK_WIDTH)));
float *A, *S, *P;
int *flags;
cudaMallocManaged(&A, n*sizeof(float));
cudaMallocManaged(&P, n*sizeof(float));
cudaMallocManaged(&S, m*sizeof(float));
cudaMallocManaged(&flags, m*sizeof(int));
for (unsigned int i = 0; i < m; i++) S[i] = 0.0;
for (unsigned int i = 0; i < m; i++) flags[i] = 0;
flags[0] = 1;
prefix_sum<<<m, BLOCK_WIDTH,
(BLOCK_WIDTH*COARSE_FACTOR + BUFFER)*sizeof(float)>>>(A, P, flags, S, n, m);
cudaDeviceSynchronize();
}
You can find more details about memory padding and bank memory conflicts in the following blog:
Parallel Prefix Sum
There is a very minute change in performance after this change indicating that most performance bottleneck is the block serialization part.